1. Бассейн имеет форму прямоугольного параллелепипеда. Его длина, ширина и
глубина равны соответственно 25 м, 12 м и 2 м. Для облицовки дна и стен бассейна
решено приобрести плитку по цене 500 р. за квадратный метр. Сколько рублей будет
стоить покупка, если по периметру бассейна дополнительно планируется выложить
прямоугольную дорожку шириной 1 м из той же плитки?
Смотреть решение
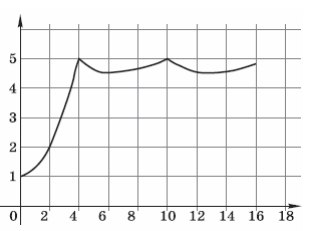
2. На графике показано изменение давления в паровой турбине после запуска. На оси
абсцисс откладывается время в минутах, на оси ординат — давление в атмосферах.
Определите по графику, сколько минут прошло от запуска турбины до момента,
когда давление в первый раз достигло наибольшего значения.
Смотреть решение
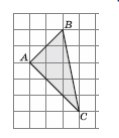
3. Найдите площадь треугольника ABC, если сторона клетки равна 4.
Смотреть решение
4. На прилавке лежат 8 одинаковых пар перчаток, но у одной пары есть незаметный
снаружи брак внутри обеих перчаток. В ходе примерок все перчатки перемешались.
Продавец разделил все перчатки случайным образом на 4 группы по 4 штуки. Какова
вероятность того, что обе бракованные перчатки находятся в одной группе?
Смотреть решение
5. Решите уравнение \( \sqrt{x^2+16}=3x-4 \) Если уравнение имеет более одного
корня, в ответе укажите меньший из корней.
Смотреть решение
6. Найдите острый угол между биссектрисами острых углов прямоугольного
треугольника. Ответ дайте в градусах
Смотреть решение
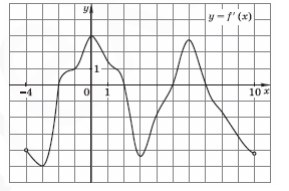
7. На рисунке изображён график y=f′(x) производной функции y=f(x) определённой на интервале (-4;10). Найдите количество точек, в которых касательная к графику y=f(x) параллельна прямой y=x или совпадает с ней.
Смотреть решение
8. Высота правильной треугольной пирамиды втрое меньше стороны основания.
Найдите угол между боковым ребром и плоскостью основания пирамиды. Ответ дайте
в градусах.
Смотреть решение
9. Найдите значение выражения \( x+2^{3x+2}*8^{-x} \) при \( x=6 \)
Смотреть решение
10. После дождя уровень воды в колодце может повыситься. Мальчик определяет
его, измеряя время падения t небольших камушков в колодец и рассчитывая по
формуле \( h=5t^2 \) . До дождя время падения камушков составляло 1,4 с. На какую
минимальную высоту должен подняться уровень воды после дождя, чтобы
измеряемое время изменилось больше чем на 0,2 с?
Смотреть решение
11. Из точки А круговой трассы одновременно начинают равномерное движение в
противоположных направлениях два тела. К моменту их встречи первое тело проходит
на 200 м больше, чем второе, и возвращается в точку А через 25 мин после встречи.
Найдите длину трассы в метрах, если второе тело возвращается в точку А через 36 мин
после встречи.
Смотреть решение
12. Найдите наименьшее значение функции \( y=\frac{x^2-8x+64}{x} \) на [4;18].
Смотреть решение
