1. Одна таблетка лекарства весит 40 мг и содержит 6% активного вещества. Ребёнку в
возрасте до 6 месяцев врач прописывает 1,2 мг активного вещества на каждый
килограмм веса в сутки. Сколько таблеток этого лекарства следует дать ребёнку в
возрасте четырёх месяцев и весом 6 кг в течение суток?
Смотреть решение
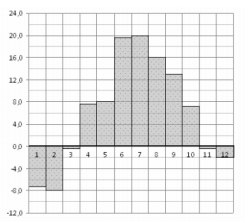
2. На диаграмме показана среднемесячная температура воздуха в Санкт‐
Петербурге за каждый месяц 1999 года. По горизонтали указываются месяцы, по
вертикали – температура в градусах Цельсия. Определите по диаграмме, сколько
было месяцев с положительной среднемесячной температурой.
Смотреть решение
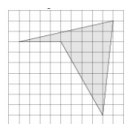
3. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Смотреть решение
4. Чтобы пройти в следующий круг соревнований, футбольной команде нужно
набрать хотя бы 6 очков в двух играх. Если команда выигрывает, она получает 4 очка, в
случае ничьей – 2 очка, если проигрывает – 0 очков. Найдите вероятность того, что
команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре
вероятности выигрыша и проигрыша одинаковы и равны 0,3.
Смотреть решение
5. Найдите корень уравнения \( (2x+5)^{\frac{1}{3}}=-3 \)
Смотреть решение
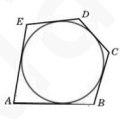
6. Около окружности, радиус которой равен 2, описан многоугольник, периметр которого равен 36. Найдите его площадь.
Смотреть решение
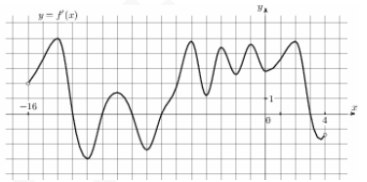
7. На рисунке изображен график у=f′(x) – производной функции у=f (x),
определенной на интервале (−16; 4). Найдите количество точек экстремума функции
у=f (x), принадлежащих отрезку [−14; 2].
Смотреть решение
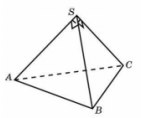
8. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.
Смотреть решение
9. Найдите значение выражения \( sin\frac{7π}{6}cos\frac{5π}{3} \)
Смотреть решение
10. Перед отправкой тепловоз издал гудок с частотой f0 = 490 Гц. Чуть позже издал
гудок подъезжающий к платформе тепловоз. Из‐за эффекта Доплера частота второго
гудка f больше первого: она зависит от скорости тепловоза по закону \( f(v)=\frac{f_{0}}{1-\frac{v}{c}} \)(Гц), где с – скорость звука в воздухе (в м/с). Человек, стоящий на
платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц.
Определите, с какой минимальной скоростью приближался к платформе тепловоз,
если человек смог различить сигналы. Считать, что с=340 м/с. Ответ выразите в м/с.
Смотреть решение
11. Имеется два сосуда. Первый содержит 100 кг, а второй – 20 кг раствора кислоты
различной концентрации. Если эти растворы смешать, то получится раствор,
содержащий 67% кислоты. Если же смешать равные массы этих растворов, то
получится раствор, содержащий 77% кислоты. Сколько килограммов кислоты
содержится в первом сосуде?
Смотреть решение
12. Найдите наименьшее значение функции \( y=(x^2-4x+4)*e^x \) на отрезке [-1;3].
Смотреть решение
