13. а) Решите уравнение \( cos2x+\sqrt{2}*cos(x+\frac{5π}{4})=sinx \)
Б) Найдите все корни этого уравнения, принадлежащие отрезку \( [6π;\frac{15π}{2}] \)
Смотреть решение
14. В прямоугольном параллелепипеде ABCDA1B1C1D1 АВ=5, AD=6, AA1=8, точка К –середина ребра DD1
А) Докажите, что прямые ВС и КС1 перпендикулярны.
Б) Найдите отношение объемов, на которые делится прямоугольный параллелепипед
плоскостью ВКС1
Смотреть решение
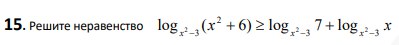
Смотреть решение *
16. Серединный перпендикуляр к стороне АВ треугольника АВС пересекает сторону
АС в точке D. Окружность с центром О, вписанная в треугольник ADB , касается отрезка
AD в точке Р , а прямая ОР пересекает сторону АВ в точке К .
а) Докажите, что около четырехугольника ВDОК можно описать окружность.
б) Найдите радиус этой окружности, если АВ = 10, АС = 8, ВС = 6.
Смотреть решение
17. В июле планируется взять кредит в банке на сумму 4 млн рублей на срок 10 лет.
Условия его возврата таковы:
— каждый январь долг возрастает на r% по сравнению с концом предыдущего года;
— с февраля по июнь необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на
июль предыдущего года.
Найдите % , если известно, что наибольший годовой платёж по кредиту составит не
более 1,16 млн рублей, а наименьший — не менее 0,476 млн рублей.
Смотреть решение
