1. Для приготовления маринада для огурцов на 1 литр воды требуется 12 г лимонной кислоты. Лимонная кислота продается в пакетиках по 10 г. Какое наименьшее число пакетиков нужно купить хозяйке для приготовления 8 литров маринада?
Смотреть решение
2. На рисунке жирными точками показана среднемесячная цена нефти во все месяцы
1998 и 1999 года. По горизонтали указываются месяцы, по вертикали – цена барреля
нефти в долларах США. Для наглядности жирные точки на рисунке соединены линией.
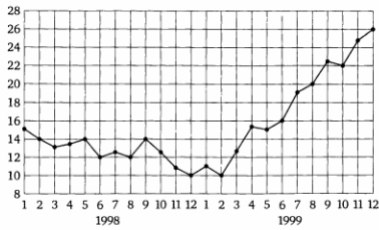
Определите по рисунку, во сколько раз среднемесячная цена нефти в августе 1999
года превосходила среднемесячную цену нефти в декабре 1998 года.
Смотреть решение
3. Площадь квадрата, вписанного в круг, равна 3. Найдите площадь квадрата, описанного около этого круга.
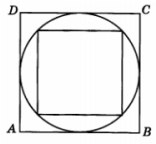
Смотреть решение
4. Бросают два игральных кубика. Найдите вероятность того, что произведение
выпавших очков больше или равно 10. Ответ округлите до сотых.
Смотреть решение
5. Решите уравнение \( 5^x*2^{-x}=0,4 \)
Смотреть решение
6. На сторонах AB и BC треугольника ABC выбраны соответственно точки P и Q так, что BP_PA=1:2 и BQ_QC=4:1. Найдите отношение площади четырёхугольника ACQP к
площади треугольника PBQ.
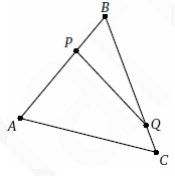
Смотреть решение
7. На рисунке изображен график функции y=f(x) определенной на интервале (-10;3). Найдите количество точек, в которых касательная к графику функции параллельна прямой y=-3.
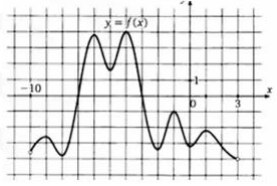
Смотреть решение
8. Найдите объем многогранника, вершинами которого являются вершины A, B, C, A1, B1, C1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 6, а боковое ребро равно 3.
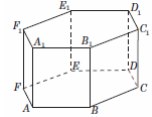
Смотреть решение
9. Найдите значение выражения \( x+6^{2x+1}:36^x \) при \( x=5 \)
Смотреть решение
10. Мяч бросили под острым углом α к горизонту. Время полета мяча, выраженная
в секундах, определяется по формуле \( t=\frac{2V_{0}sina}{g} \) . При каком наименьшем
значении (в градусах) время полета будет не меньше 1,7 секунды, если мяч
бросают с начальной скоростью \( V_{0}=\frac{17}{\sqrt{3}} \) м/c? Ускорение свободного падения g считайте равным 10 м/c2.
Смотреть решение
11. Первые 140 км автомобиль проехал со скоростью 50 км/ч, следующие 160 км – со скоростью 60 км/ч, а затем 120 км – со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Смотреть решение
12. Найдите точку максимума функции \( y=11+6\sqrt{x}-2x\sqrt{x} \)
Смотреть решение
