13. А) Решите уравнение \( sinx+cos(5x-4,5π)=\sqrt{3}sin(3x+π) \)
Б) Найдите корни, принадлежащие отрезку [-π;0,5π]
Смотреть решение
14. В основании прямой призмы ABCDA1B1C1D1 лежит ромб ABCD, причем AB=BD.
Точки М и N – середины ребер В1С1 и АВ соответственно.
А) Докажите, что сечение призмы плоскостью MND1 – многоугольник с прямым углом
при вершине D1.
Б) Найдите площадь указанного сечения, если AB=8, AA1=3√2
Смотреть решение
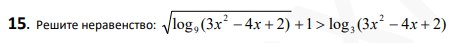
Смотреть решение *
16. Дана трапеция ABCD с основаниями AD и ВС. Диагонали АС и BD пересекаются в
точке О, а прямые АВ и CD – в точке К. Прямая КО пересекает стороны ВС и AD в точках
М и N соответственно, и угол BAD равен 300. Известно, что в трапеции ABMN и NMCD
можно вписать окружность.
А) Докажите, что треугольник AKD тупоугольный.
Б) Найти отношение площадей треугольника ВКС и трапеции ABCD
Смотреть решение
17. На счет, который вкладчик имел в начале первого квартала, начисляется в конце
этого квартала r1% , а на счет, который вкладчик имел в начале второго квартала,
начисляется в конце этого квартала r2% , причем r1+r2=150% Вкладчик положил
на счет в начале первого квартала некоторую сумму и снял в конце того же квартала
половину этой суммы. При каком значении r1 счет вкладчика в конце второго квартала
окажется максимально возможным?
Смотреть решение
