13. Дано уравнение √sin2x=2^(1/4)*√cosx
А) Решите уравнение.
Б) Укажите корни этого уравнения, принадлежащие отрезку [-1,5π;0]
Смотреть решение
14. В основании прямой призмы ABCDA1B1C1D1 лежит прямоугольная
трапеция АВСD с основаниями ВС и АD (ВС < АD), в которой АВ=5, CD=4, ВС=6. Через
точку С и середину ребра ВВ1 параллельно B1D проведена плоскость β.
А) Докажите, что плоскость β пересекает ребро АА1 в такой точке Р, что А1Р=3АР.
Б) Найдите объем пирамиды с вершиной в точке В, основанием которой служит
сечение призмы плоскостью β, если известно, что ВВ1=16.
Смотреть решение
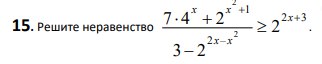
Смотреть решение1 Продолжение
16. На стороне ВС треугольника АВС отмечена точка К. Оказалось, что отрезок АК
пересекает медиану ВD в точке Е так, что АЕ=ВС.
А) Докажите, что ВК=КE.
Б) Найдите площадь четырехугольника CDEК, если известно, что АВ=13, АЕ=7, АD=4.
Смотреть решение
17. Олигарх Аристарх Луков‐Арбалетов имеет в собственности три частных банка. Активы первого банка состоят на 70% из рублей и на 30% из долларов. Во втором банке 80% активов составляют рубли и 20% – евро; в третьем банке 50% активов в
рублях, 10% – в долларах и 40% – в евро. Аристарх планирует открыть 4‐й банк, направив туда часть активов из каждого банка так, чтобы доля каждой валюты в каждом из них сохранилась, а активы нового банка состояли бы ровно на 15% в
долларах. Какой наименьший процент рублей могут содержать активы нового банка?
Смотреть решение
