13. А) Решите уравнение \( (log_{3}\frac{3}{x})*log_{2}x-log_{3}\frac{x^3}{\sqrt{3}}=1/2+log_{2}\sqrt{x} \)
Б) Найдите корни, принадлежащие отрезку [0;0,2]
Смотреть решение
14. В основании треугольной пирамиды ABCD лежит треугольник АВС, где АВ=ВС=5,
АС=6. Боковые ребра наклонены к плоскости основания под углом, синус которого
равен 3/4.
А) Постройте сечение, проходящее через центр описанной окружности основания и
перпендикулярное прямой BD
Б) Найдите расстояние от прямой BD до прямой АС.
Смотреть решение
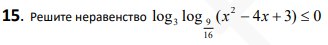
Смотреть решение
16. Дан прямоугольник ABCD. Окружность с центром в точке В и радиусом АВ
пересекает продолжение стороны АВ в точке М. Прямая МС пересекает прямую AD в
точке К, а окружность во второй раз в точке F.
А) Докажите, что DK=DF
Б) Найдите КС, если BF=20, DF=21
Смотреть решение
17. Ученики второго, третьего четвертого классов собирали макулатуру. Каждый
второклассник работал по 3 дня, третьеклассник – по 12 дней, четвероклассник – по 16
дней. При этом каждый второклассник собрал 30 кг макулатуры, каждый третьеклассник
– 130 кг, а каждый четвероклассник – 170 кг. Все дети вместе отработали 95 дней.
Сколько учеников каждого класса участвовало в работе, если общее количество
макулатуры оказалось максимальным?
Смотреть решение
