1. В сентябре 1 кг винограда стоил 60 рублей, в октябре виноград подорожал на 25%, а в ноябре еще на 20%. Сколько рублей стоил 1 кг винограда после подорожания в ноябре?
Смотреть решение
2. При работе фонарика батарейка постепенно разряжается, и напряжение в электрической цепи фонарика падает. На рисунке показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечается время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по рисунку, на сколько вольт упадёт напряжение за 15 часов работы фонарика.
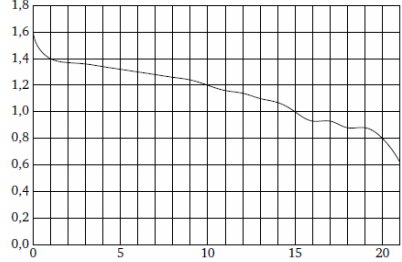
Ответ: 0,6
3. На клетчатой бумаге изображён угол BDE. Найдите
его величину. Ответ выразите в градусах
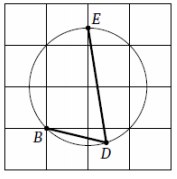
Смотреть решение
4. Восемь различных книг расставляются наудачу на одной полке. Найти вероятность
того, что две определенные книги окажутся поставленные рядом.
Смотреть решение
5. Решите уравнение \( log_{6-x}81=2 \). Если уравнение имеет более одного корня, в
ответе укажите больший из них.
Смотреть решение
6. На боковой стороне CB равнобедренного (AB=BC) треугольника
ABC выбрана точка K. Оказалось, что CA=AK=KB. Найдите ∠ABC.
Ответ дайте в градусах.

Смотреть решение
7. На рисунке изображен график производной функции f(x), определенной
на интервале (−2; 11). Найдите точку экстремума функции f (x), принадлежащую
отрезку [1; 6].
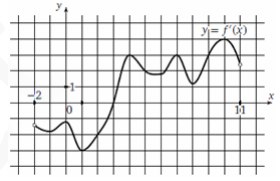
Смотреть решение
8. Найдите площадь поверхности многогранника, изображенного на рисунке. Все двугранные углы
многогранника прямые.
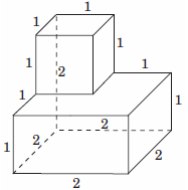
Смотреть решение
9. Найдите значение выражения \( 4\sqrt{6}cos\frac{3π}{4}*sin\frac{3π}{4} \)
Смотреть решение
10. Ёмкость высоковольтного конденсатора в телевизоре C = 3 ∙ 10‐6 Ф. Параллельно с конденсатором подключён резистор с сопротивлением R = 5 ∙ 106 Ом. Во время работы телевизора напряжение на конденсаторе U0=9 кВ. После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за время (в секундах),
определяемое выражением \( t=aRC*log_{2}\frac{U_{0}}{U} \) где α = 1,1—постоянная. Определите (в киловольтах) наибольшее возможное напряжение на конденсаторе, если после выключения телевизора прошло не менее 33 с.
Смотреть решение
11. Имеются два сплава. Первый сплав содержит 45% меди, второй – 20% меди. Масса первого сплава больше массы второго на 30 кг. Из этих двух сплавов получили третий сплав, содержащий 40% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Смотреть решение
12. Найдите наименьшее значение функции \( y=\frac{\sqrt{3}}{3}π-2cosx-\sqrt{3}x-5 \) на [0;0.5π]
Смотреть решение
