13. А) Решите уравнение 3sin^2x-cos(9π/2-x)*sin(3π/2+x)-2=0
Б) Найдите корни, принадлежащие отрезку [3π;4π]
Смотреть решение
14. В прямоугольном параллелепипеде ABCDA1B1C1D1 известны ребра АВ=6, AD=12,
AA1=10. Точка Е принадлежит отрезку BD, причем ВЕ:ED=1:2. Плоскость a проходит
через точки А, Е и середину ребра ВВ1
А) Докажите, что сечение параллелепипеда плоскостью a является равнобедренным
треугольником.
Б) Найдите расстояние от точки В1 до плоскости сечения
Смотреть решение
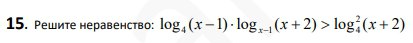
Смотреть решение *
16. Из вершин А и В тупоугольного треугольника АВС проведены высоты BQ и AH.
Известно, что угол В – тупой, BC:CH=4:5, BH=BQ
А) Докажите, что диаметр описанной вокруг треугольника ABQ окружности в \( \frac{2\sqrt{6}}{3} \) раз больше BQ
Б) Найдите площадь четырехугольника AHBQ, если площадь треугольника HQC равна
25
Смотреть решение
17. Руслан вложил 1 млн. в банк под 14% годовых (начисление в конце года на общую
сумму). При этом каждый месяц он снимает по Х тыс. рублей на проживание (начиная со
2 года) в течении 4 лет, и в конце 5 года после начисления процентов сумма оказалась
не менее 1 млн. Определите какую максимальную сумму он мог снимать ежемесячно. В
ответе укажите целочисленное значение в тысячах рублей?
Смотреть решение
