1. Большой корабль не может подойти к берегу, поэтому пассажиров отвозят с
корабля на шлюпке, вмещающей 8 пассажиров. Сколько раз шлюпка приставала к
берегу, если на берег отвезли 30 пассажиров?
Смотреть решение
2. На рисунке жирными точками показаны среднесуточная температура в Москве в
период с 12 июля 2010 года по 11 августа 2010 года и климатические нормы
среднесуточной температуры за соответствующий период. По горизонтали
указываются дни, по вертикали — температура в градусах Цельсия. Для наглядности
жирные точки, соответствующие среднесуточной температуре, соединены сплошной
линией, а точки, соответствующие климатической норме, — пунктирной линией.
Определите по рисунку наименьшую среднесуточную температуру с 1 по 11 августа.
Ответ дайте в градусах Цельсия.
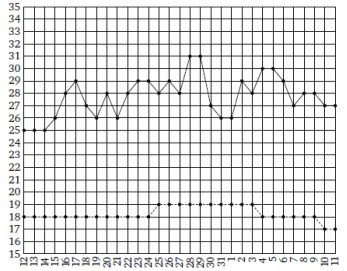
Ответ: 26
3. На клетчатой бумаге изображена фигура. Найдите
∠ ABD-∠ ACD . Ответ выразите в градусах.
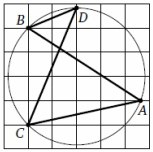
Смотреть решение
4. На столе лежат 10 карточек, на которых написаны числа от 1 до 10. Даша случайно
вытягивает одну карточку. С какой вероятностью число на выбранной карточке больше
7?
Смотреть решение
5. Решите уравнение: \( cos\frac{πx}{7}=-1 \) В ответе запишите наибольший отрицательный корень уравнения.
Смотреть решение
6. В треугольнике ABC проведена биссектриса AL. Известно,
что ∠ACB = 30° и ∠ BAL = 22°. Найдите ∠ ABC. Ответ дайте
в градусах.
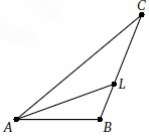
Смотреть решение
7. На рисунке изображен график y=F(x) одной из первообразных некоторой функции f(x) ,
определенной на интервале (‐1;13). Определите количество целых чисел x для которых f(x)
отрицательно.
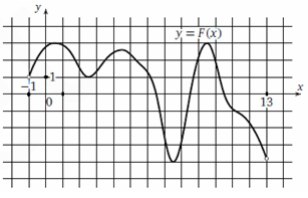
Смотреть решение
8. Прямоугольник ABCD, у которого AB=4, AD=3, вращается вокруг прямой AD.
Найдите площадь S поверхности тела вращения. В ответе укажите S/π
Смотреть решение
9. Найдите значение выражения \( 1,75^{\frac{1}{9}}*4^{\frac{2}{9}}*28^{\frac{8}{9}} \)
Смотреть решение
10. На верфи инженеры проектируют новый подводный зонд для изучения морских
глубин. Конструкция будет крепиться ко дну при помощи троса. Зонд имеет
кубическую форму, а значит, сила натяжения троса определяется по формуле:
T=pgl^3-mg где l —линейный размер аппарата в метрах, ρ=1000 кг/м3—
плотность воды, g—ускорение свободного падения (считайте g=10 Н/кг), а m=83кг—
масса зонда. Каковы могут быть максимальные линейные размеры зонда, чтобы
обеспечить его эксплуатацию в условиях, когда сила натяжения троса будет не
больше, чем 2600 Н? Ответ выразите в метрах.
Смотреть решение
11. По морю параллельными курсами в одном направлении следуют два сухогруза:
первый длиной 120 метров, второй ‐ длиной 80 метров. Сначала второй сухогруз
отстает от первого, и в некоторый момент времени расстояние от кормы первого
сухогруза до носа второго сухогруза составляет 400 метров. Через 12 минут после этого
уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза
до носа первого равно 600 метрам. На сколько километров в час скорость первого
сухогруза меньше скорости второго?
Смотреть решение
12. Найдите наибольшее значение функции \( y=5-(x-14)\sqrt{x+13} \) на отрезке [-9;3]
Смотреть решение
