1. В школе №1 уроки начинаются в 8:30, каждый урок длится 45 минут, все перемены,кроме одной, длятся 10 минут, а перемена между вторым и третьим уроком—20 минут. Сейчас на часах 13:00. Через сколько минут прозвенит ближайший звонок с
урока?
Смотреть решение
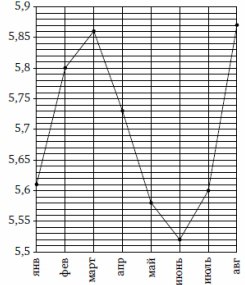
2. На рисунке жирными точками показан среднемесячный курс китайского юаня с
января по август 2014 года. По горизонтали указываются месяцы, по вертикали — цена
юаня в рублях. Для наглядности жирные точки соединены линией. Определите по
рисунку разность курса юаня в августе и июле. Ответ дайте в рублях.
Смотреть решение
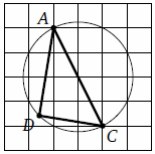
3. На клетчатой бумаге изображён треугольник ADC,
вписанный в окружность. Найдите угол ADC. Ответ
выразите в градусах.
Смотреть решение
4. Аня и Таня выбирают по одному натуральному числу от 1 до 9 независимо друг отдруга. Найдите вероятность того, что сумма этих чисел делится на 3. Ответ сократите до сотых.
Смотреть решение
5. Решите уравнение \( \sqrt{19+6x}=x+4 \) . Если уравнение имеет более одного корня,
то в ответе укажите меньший из них.
Смотреть решение
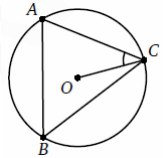
6. Точка O—центр описанной окружности остроугольного
треугольника ABC. Найдите ABC, если OCA=37◦. Ответ
дайте в градусах.
Смотреть решение
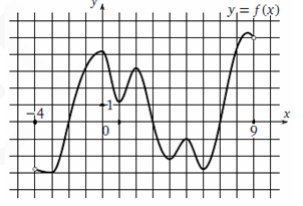
7. На рисунке изображен график функции y=f(x), определенной на
интервале (−4; 9). Определите количество целых чисел x , для
которых f′(x) отрицательно.
Смотреть решение
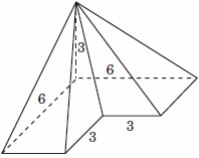
8. Найдите объем пирамиды, изображенной на
рисунке. Ее основанием является многоугольник,
соседние стороны которого перпендикулярны, а
одно из боковых ребер перпендикулярно
плоскости основания и равно 3.
Смотреть решение
9. Найдите значение выражения \( 16^{\frac{1}{3}}*16^{\frac{1}{6}} \)
Смотреть решение
10. Катер должен пересечь реку шириной L=100 м так, чтобы причалить точно напротив места отправления. Скорость течения реки u=0,5 м/с. Время в пути, измеряемое в секундах, равно\( t=\frac{L}{u}ctga \), где α—острый угол между осью катера и
линией берега. Под каким минимальным углом α к берегу нужно направить катер, чтобы время в пути было не больше 200 с? Ответ дайте в градусах.
Смотреть решение
11. Первую треть трассы велосипедист ехал со скоростью 12 км/ч, вторую треть—со скоростью 16 км/ч, а последнюю треть—со скоростью 24 км/ч. Найдите среднюю скорость велосипедиста на протяжении всего пути. Ответ дайте в км/ч.
Смотреть решение
12. Найдите наибольшее значение функции \( y=\frac{x^2+7x+49}{x} \) на отрезке [-14;-1]
Смотреть решение
