13. а) Решите уравнение: sin^2x+3x^2cosx+3x^2=0
б) Укажите корни этого уравнения, принадлежащие отрезку [-0.5pi;pi]
Смотреть решение
14. Основанием пирамиды FABCD является квадрат ABCD. На ребре AF взята точка Е
такая, что отрезок СЕ перпендикулярен ребру AF. Проекция О точки Е на основание
пирамиды лежит на отрезке АС и делит его в отношении AO:OC=4:1. Угол ADF равен
900.
А) Докажите, что ребро FC перпендикулярно плоскости основания пирамиды
Б) Найдите разность объемов пирамид FABCD и EABD, если известно, что АВ=1.
Смотреть решение
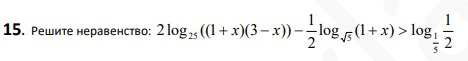
Смотреть решение *
16. В треугольнике АВС точка D есть середина АВ, точка Е лежит на стороне ВС,
причем BE=1/3*BC. Отрезки АЕ и CD пересекаются в точке О.
А) Доказать, что AO/OE=3/2
Б) Найти длину стороны АВ, если АЕ=5, ОС=4, а угол АОС равен 120
Смотреть решение
17. В пчелиной семье, зимующей в помещении, в день последней весенней
подкормки было 9 тысяч пчел. К концу k ‐го дня ( k=1,2,3… ) после дня подкормки
численность пчелиной семьи, зимующей в помещении, становится равной
тысяч пчел. Далее, при перевозке пчел на летнюю стоянку, численность пчелиной семьи
в каждый последующий день возрастает на 25% по сравнению с предыдущим днем. В
конце какого дня после весенней подкормки нужно перевезти пчел на летнюю стоянку,
чтобы через 38 дней после подкормки численность пчелиной семьи стала наибольшей?
Известно, что у фермера нет возможности поместить пчел на летнюю стоянку сразу же
после подкормки.
Смотреть решение
