13. а) Решите уравнение: \( 4(sin4x-sin2x)=sinx(4cos^23x+3) \)
б) Укажите корни этого уравнения, принадлежащие отрезку \( [0; 1.5π] \)
Смотреть решение
14. В основании пирамиды TABCD лежит трапеция ABCD , в которой ВС||AD и
AD_BC=2. Через вершину Т пирамиды проведена плоскость, параллельная прямой ВС и
пересекающая отрезок АВ в точке М такой, что АМ:MB=2. Площадь получившегося
сечения равна 10, а расстояние от ребра ВС до плоскости сечения равно 4.
А) Докажите, что плоскость сечения делит объем пирамиды в отношении 7:20
Б) Найдите объем пирамиды.
Смотреть решение
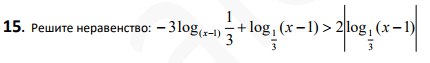
Смотреть решение, продолжение *
16.
16. Радиус вписанной в треугольник АВС окружности равен \( \frac{\sqrt{15}}{3} \) . Окружность радиуса \( \frac{5\sqrt{15}}{3\sqrt{3}} \)
касается вписанной в треугольник АВС окружности в точке Т, а также
касается лучей, образующих угол АСВ.
Окружности касаются прямой АС в точках К и М.
А) Докажите, что треугольник КТМ прямоугольный
Б) Найдите тангенс угла АВС, если площадь треугольника АВС равна 153 , а
наибольшей из его сторон является сторона АС.
Смотреть решение
17. Фермер получил кредит в банке под определенный процент годовых. Через год
фермер в счет погашения кредита вернул в банк 3/4 от всей суммы, которую он был
должен банку к этому времени, а еще через год в счет полного погашения кредита он
внес в банк сумму, на 21% превышающую величину полученного кредита. Каков
процент годовых по кредиту в банке?
Смотреть решение
