1. В сентябре 1 кг винограда стоил 60 рублей, в октябре виноград подорожал на 25%,
а в ноябре еще на 20%. Сколько рублей стоил 1 кг винограда после подорожания в
ноябре?
Смотреть решение
2. На рисунке примерно изображена «демографическая пирамида», отображающая
половозрастной состав населения Объединенных Арабских Эмиратов в 2000 году. По
вертикали указывается возраст, по горизонтали—количество мужчин и женщин
данного возраста.
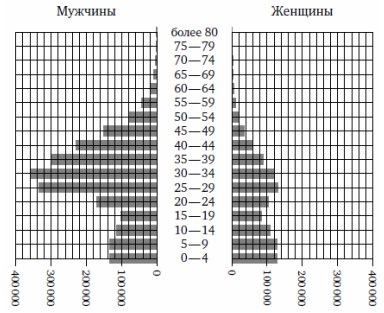
Пользуясь диаграммой, определите, сколько человек в возрасте 50—54 лет
проживало в Объединенных Арабских Эмиратах в 2000 году.
Ответ: 100000
3. На клетчатой бумаге с размером клетки 1 × 1 изображён
равносторонний треугольник ABC. Найдите радиус вписанной в
него окружности.
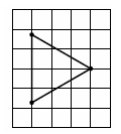
Смотреть решение
4. В избирательный список внесены имена трех кандидатов: П., Н. и С. Порядок их в
списке определяется случайно с помощью компьютера. Найдите вероятность того, что
их имена будут расположены в списке в алфавитном порядке. Результат округлите до
сотых.
Смотреть решение
5. Решите уравнение \( log_{3}(x^2-12)=log_{3}(-x) \). Если уравнение имеет более
одного корня, в ответе укажите больший из них.
Смотреть решение
6. В треугольнике ABC известно, что A = 300 и B = 860. CD—биссектриса внешнего
угла при вершине C, причём D лежит на прямой AB. На продолжении стороны AC за
точку C выбрана точка E так, что CB = CE. Найдите ADE. Ответ дайте в градусах.
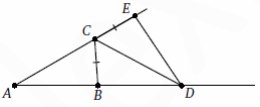
Смотреть решение
7. На рисунке изображен график движения точки по прямой. По горизонтали отложено время, по вертикали—расстояние до точки отсчета. Сколько раз за наблюдаемый период
точка останавливалась?
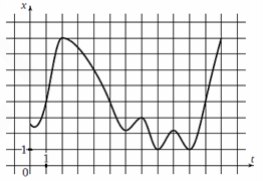
Смотреть решение
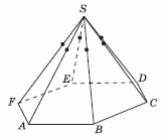
8. В правильной шестиугольной пирамиде SABCDEF
площадь основания равна 18, боковые ребра равны 9.
Проведите сечение через точки боковых ребер,
отстоящих от вершины S на расстояние 3. Найдите его
площадь.
Смотреть решение
9. Найдите значение выражения: \( \sqrt{(a-2)^2}+\sqrt{(a-4)^2} \) при 2≤a≤4
Смотреть решение
10. Автомобиль, движущийся в начальный момент времени со скоростью
\( V_{0}=30 \)м/сначал торможение с постоянным ускорением \( a=2 \) м/с^2. За t секунд
после начала торможения он прошёл путь \( S=V_{0}t-\frac{at^2}{2} \) (м). Определите время, прошедшее от момента начала торможения, если известно, что за это время
автомобиль проехал 112 метров. Ответ выразите в секундах.
Смотреть решение
11. Имеются два сосуда с растворами кислоты различной концентрации. Первый
содержит 5 кг раствора, а второй— 10 кг раствора. Если эти растворы смешать, то
получится раствор, содержащий 40% кислоты. Если же смешать равные массы этих
растворов, то получится раствор, содержащий 35%кислоты. Сколько килограммов
кислоты содержится в первом сосуде?
Смотреть решение
12. Найдите точку максимума функции \( y=sinx-4cosx-4xsinx+5 \)принадлежащую промежутку \( (0;\frac{π}{2}) \)
Смотреть решение
