13. а) Решите уравнение: \( cos(x+\frac{π}{3})+sin(x+\frac{π}{6})-cos2x=1 \)
б) Укажите корни этого уравнения, принадлежащие отрезку \( [-\frac{3π}{2}; \frac{π}{2}] \)
Смотреть решение
14. На боковых ребрах DB и DC треугольной пирамиды ABCD расположены точки М и
N так, что ВМ=MD и CN:ND=2:3. Через вершину А основания пирамиды и точки М и N
проведена плоскость, пересекающая медианы боковых граней, проведенные из
вершины D, в точках К, R и Т.
А) Докажите, что площадь треугольника KTR составляет 5/22 от площади сечения
пирамиды плоскостью
Б) Найти отношение объемов пирамид KRTC и ABCD.
Смотреть решение
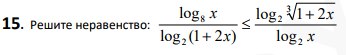
Смотреть решение *
16. Четырехугольник ABCD вписан в окружность с центром в точке О. Радиус АО
перпендикулярен радиусу ОВ, а радиус ОС перпендикулярен радиусу OD.
А) Докажите, что ВС|| AD
Б) Найдите площадь треугольника АОВ, если длина перпендикуляра, опущенного из
точки С на AD, равна 9, а длина отрезка ВС в два раза меньше длины отрезка AD.
Смотреть решение
17. Предприятие производит холодильники и является прибыльным. Известно, что при
изготовлении n холодильников в месяц расходы на выпуск одного холодильника
составляют не менее \( \frac{48000}{n}+240-|80-\frac{48000}{n}| \)тыс. руб., а цена реализации
каждого холодильника при этом не превосходит \( 480-\frac{n}{5} \) тыс.руб. Определить
ежемесячный объем производства, при котором может быть получена наибольшая при
данных условиях ежемесячная прибыль.
Смотреть решение
