13. а) Решите уравнение: \( \frac{2-3sinx-3cos2x}{6x^2-πx-π^2}=0 \)
б) Укажите корни этого уравнения, принадлежащие отрезку \( [-\frac{π}{2};\frac{2π}{3}] \)
Смотреть решение
14. Куб целиком находится в правильной треугольной пирамиде SABC с вершиной S
так, что одна грань куба принадлежит основанию, одно ребро целиком принадлежит
грани SBC, а грани SAB и SAC содержат по одной вершине куба. Известно, что ребро АВ
в 2 раза больше высоты пирамиды.
А) Докажите, что плоскость, проходящая через вершины куба, принадлежащие граням
SAB и SAC, и вершину пирамиды, перпендикулярна плоскости ASD, где D – середина
стороны ВС.
Б) Найдите отношение объемов пирамиды и куба.
Смотреть решение
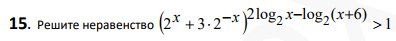
Смотреть решение *
16. Из середины D гипотенузы АВ прямоугольного треугольника АВС проведен луч,
перпендикулярный к гипотенузе и пересекающий один из катетов. На нем отложен
отрезок DE, длина которого равна половине отрезка АВ. Длина отрезка СЕ равна 1 и
совпадает с длиной одного из катетов.
А) Докажите, что угол АСЕ равен 45 градусов
Б) Найдите площадь треугольника АВС
Смотреть решение
17. В январе 2014 года Аристарх Луков‐Арбалетов взял в кредит 1 млн. рублей под 12%
годовых на четыре года. Часть денег Аристарх закопал в огороде, чтобы ежегодно гасить
проценты по кредиту. На оставшиеся деньги Аристарх купил доллары США по курсу 33
рубля за один доллар, а на половину этих долларов ‐ биткоины (BTC) по курсу 750
долларов за 1 BTC. 1 января 2018 года Аристарх продал биткоины по цене 13800
долларов США за один BTC и доллары по курсу 69 рублей за один доллар. Найдите
доход, полученный Аристархом, округлив его до целого числа млн. рублей.
Смотреть решение
