1. Тетрадь стоит 24 рубля. Сколько рублей заплатил покупатель за 60 тетрадей, если
при покупке больше 50 тетрадей магазин делает скидку 10% от стоимости всей
покупки?
Смотреть решение
2. На рисунке показано, как изменялась температура воздуха на протяжении одних
суток. По горизонтали указано время суток, по вертикали — значение температуры в
градусах Цельсия.
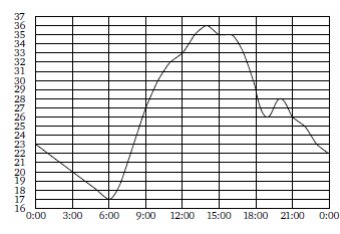
Найдите наименьшее значение температуры с 6 до 9 часов вечера. Ответ дайте в
градусах Цельсия.
Ответ: 26
3. Найдите периметр четырёхугольника ABCD с вершинами A(−7; −2), B(−7; 2), C(5; −3),
D(5; −7).
Смотреть решение
4. В одной корзине имеется 5 шаров, из которых 3 белых, 2 черных, а во второй 6
шаров – 1 белый и 5 черных. Из каждой корзины вынимают по одному шару. Найдите
вероятность того, что вынутые шары будут разного цвета. Ответ округлите до сотых
Смотреть решение
5. Решите уравнение \( \frac{x+6}{5x+9}=\frac{x+6}{9x+5} \)Если уравнение имеет более одного корня, в
отете запишите меньший из корней
Смотреть решение
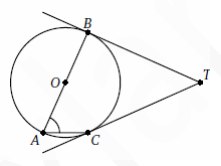
6. AB—диаметр окружности, TB и TC – касательные к ней. Найдите угол CTB, если
CAB=66◦. Ответ дайте в градусах.
Смотреть решение
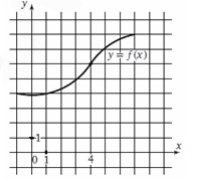
7. На рисунке изображен график функции f (x).
Касательная к этому графику, проведенная в точке с
абсциссой 4, проходит через начало координат. Найдите
f ′(4).
Смотреть решение
8. Радиусы трех шаров равны 3, 4 и 5. Найдите радиус шара, объем которого равен
сумме их объемов
Смотреть решение
9. Найдите значение выражения \( x:5^{2x+1}*25^{x-1} \) при \( x=25 \)
Смотреть решение
10. На рельсах стоит платформа. Скейтбордист прыгает на неё со скоростью м/с
под острым углом α к рельсам. От толчка платформа начинает ехать со скоростью
\( u=\frac{m}{m+M}v*cosa \)
где m = 80 кг—масса скейтбордиста со скейтом, а M =400 кг—масса платформы. Под
каким наибольшим углом α (в градусах) нужно прыгать, чтобы разогнать платформу до
скорости не менее чем 0,25 м/с?
Смотреть решение
11. Из города A в город B одновременно выехали два автомобиля: первый со
скоростью 65 км/ч, а второй—со скоростью 60 км/ч. Через 4 минуты следом за ними
выехал третий автомобиль. Найдите скорость третьего автомобиля, если известно, что
с момента, когда он догнал второй автомобиль, до момента, когда он догнал первый
автомобиль, прошло 40 минут. Ответ дайте в км/ч.
Смотреть решение
12. Найдите точку макcимума функции \( y=11+6\sqrt{x}-2x\sqrt{x} \)
Смотреть решение
