13. Решите уравнение: \( 7sin(2x-\frac{5π}{2})+9cosx+1=0 \)
б) Укажите корни этого уравнения, принадлежащие отрезку \( [-\frac{3π}{2};\frac{π}{3}] \)
Смотреть решение
14. Основание пирамиды DABC —прямоугольный треугольник ABC с прямым углом C.
Высота пирамиды проходит через середину ребра AC, а боковая грань ACD—
равносторонний треугольник.
а) Докажите, что сечение пирамиды плоскостью, проходящей через ребро BC и
произвольную точку M ребра AD,—прямоугольный треугольник.
б) Найдите расстояние от вершины D до этой плоскости, если M — середина ребра AD,
а высота пирамиды равна 6.
Смотреть решение
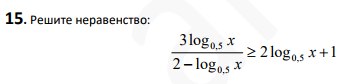
Смотреть решение *
16. Площадь трапеции ABCD равна 30. Точка Р – середина боковой стороны АВ. Точка
R на боковой стороне CD выбрана так, что 2CD=3RD. Прямые AR и PD
пересекаются в точке Q , AD=2BC.
А) Докажите, что точка Q – середина отрезка AR
Б) Найдите площадь треугольника APQ.
Смотреть решение
