1. Когда Аристарх Луков‐Арбалетов сдал ОГЭ, друзья подарили ему 10 биткоинов.
Сколько раз Аристарх может оплатить 6‐летннее обучение в ВУЗе, если стоимость
обучения 300 тыс. рублей за год, к моменту оплаты курс биткоина был 17000 долларов
США, а один доллар стоил 57 рублей?
Смотреть решение
2. На графике показано изменение курса биткоина к доллару США за некоторый
период времени. Определите по графику разность между наибольшей и наименьшей
стоимостью биткоина за указанный период в рублях по курсу 57 рублей за один
доллар США.
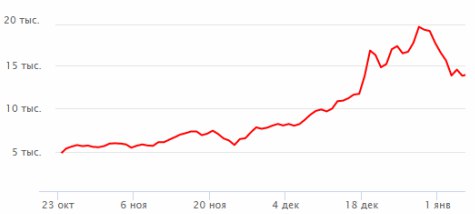
Ответ: 855000
3. На клетчатой бумаге (сторона клетки 1 см) изображён
четырёхугольник. Найдите его площадь. Ответ выразите в
квадратных сантиметрах.
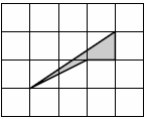
Смотреть решение
4. Аристарх Луков‐Арбалетов совершает прогулку из точки A по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Часть маршрутов приводит к поселку S, другие—в поле F или в болото M. Найдите вероятность того, что Аристарх забредет в болото. Результат округлите до
сотых.
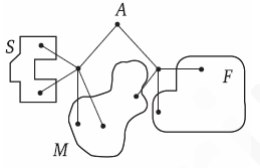
Смотреть решение
5. Решите уравнение \( \sqrt{10-3x}=x-2 \) Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Смотреть решение
6. Четырёхугольник ABCD вписан в окружность, причём
BC =CD. Известно, что угол ADC равен 930. Найдите, под
каким острым углом пересекаются диагонали этого
четырёхугольника. Ответ дайте в градусах.
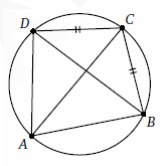
Смотреть решение
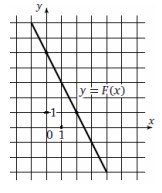
7. Прямая, изображенная на рисунке, является графиком
одной из первообразных функции. Найдите f(2)
Смотреть решение
8. В правильной треугольной призме ABCA1B1C1 , стороны
оснований которой равны 2, боковые ребра равны 1,
проведите сечение через вершины ABC1 . Найдите его
площадь.
Смотреть решение
9. Найдите значение выражения: \( \frac{b^3*b^{\frac{1}{12}}}{b^{\frac{1}{21}}*b^{\frac{1}{28}}} \)при \( b=4 \)
Смотреть решение
10. Камнеметательная машина выстреливает камни под некоторым острым углом к
горизонту с фиксированной начальной скоростью. Траектория полёта камня в системе
координат, связанной с машиной, описывается формулой \( y=ax^2+bx \), где
\( a=-\frac{1}{25} \), \( b=\frac{7}{5} \) постоянные параметры, x (м)—смещение камня по
горизонтали, y (м)—высота камня над землёй. На каком наибольшем расстоянии (в
метрах) от крепостной стены высотой 9 м нужно расположить машину, чтобы камни
пролетали над стеной на высоте не менее 1 метра?
Смотреть решение
11. Из городов A и B навстречу друг другу одновременно выехали с постоянными
скоростями два автомобиля. Скорость первого автомобиля была в два раза больше
скорости второго. Второй автомобиль прибыл в A на 1 час позже, чем первый прибыл
в B. На сколько минут раньше произошла бы встреча автомобилей, если бы второй
автомобиль ехал с той же скоростью, что и первый?
Смотреть решение
12. Найдите наименьшее значение функции \( y=\frac{x^2-6x+36}{x} \) на отрезке \( [3;9] \)
Смотреть решение
