13. Дано уравнение \( 2cos^42x-cos2x-3=0 \) А) Решите уравнение.
Б) Укажите корни этого уравнения, принадлежащие отрезку \( [-3π ;-π ] \)
Смотреть решение №1 Смотреть продолжение №2 *
14. В прямоугольном параллелепипеде ABCDA1B1C1D1 АВ=ВС=4, СС1=8. Точка
К – середина ребра АВ, точка М – середина ребра ВС. Точка Р лежит на ребре DD1 так,
что DP:PD1=3:5.
А) Докажите, что плоскость КМР перпендикулярна прямой DВ1.
Б) Найдите объем пирамиды, основанием которой является сечение параллелепипеда
плоскостью КМР, а вершиной – точка D.
Смотреть решение
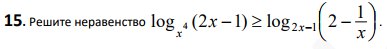
Смотреть решение
16. В треугольнике ABC на AB, как на диаметре, построена окружность ω1, а на AC, как на диаметре, построена окружность ω2. Окружности ω1 и ω2 пересекаются в точке М, отличной от точек А, В и С. А) Докажите, что точки М, В и С лежат на одной прямой. Б). Пусть АМ = 6, а диаметр окружности, описанной около треугольника АВС, равен 10. Найдите произведение АВ*АС.
Смотреть решение *
