1. Установка двух счётчиков воды (холодной и горячей) стоит 2000 рублей. До
установки счётчиков за воду платили 1500 рублей ежемесячно. После установки
счётчиков ежемесячная оплата воды стала составлять 1200 рублей. Через какое
наименьшее количество месяцев экономия по оплате воды превысит затраты на
установку счётчиков, если тарифы на воду не изменятся?
Смотреть решение
2. На диаграмме показана среднемесячная температура воздуха в Санкт‐Петербурге
за каждый месяц 1999 года. По горизонтали указываются месяцы, по вертикали –
температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев с
положительной среднемесячной температурой.
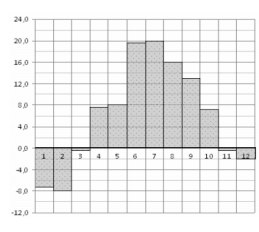
Ответ: 7
3. На клетчатой бумаге с размером клетки 1 × 1
изображён равнобедренный прямоугольный
треугольник. Найдите длину его медианы, проведённой
к гипотенузе.
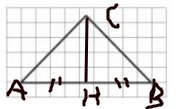
Смотреть решение
4. На фабрике керамической посуды 15% произведённых тарелок имеют дефект. При
контроле качества продукции выявляется 70% дефектных тарелок. Остальные
тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная
при покупке тарелка не имеет дефектов. Ответ округлите до сотых.
Смотреть решение
5. Найдите корень уравнения: \( 100^{x+5}=\frac{1}{1000} \)
Смотреть решение
6. Окружность, вписанная в равнобедренный треугольник,
делит в точке касания одну из боковых сторон на два отрезка,
длины которых равны 18 и 12, считая от вершины,
противолежащей основанию. Найдите периметр треугольника.
Смотреть решение
7. На рисунке приведен график функции у=g(x). На графике отмечены шесть точек: х1,
х2, …, х6. В скольких из этих точек производная g/(x) принимает положительные
значения?
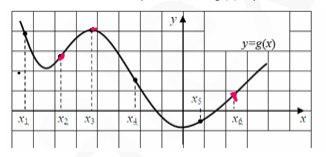
Ответ: 3
8. Найдите объем призмы, в основаниях которой лежат
правильные шестиугольники со сторонами 2, а боковые ребра
равны \( 2\sqrt{3} \) и наклонены к плоскости основания под углом 30°
Смотреть решение
9. Найдите значение выражения \( \frac{2sin68}{cos34*cos124} \)
Смотреть решение
10. Автомобиль, масса которого равна m = 1800 кг, начинает двигаться с ускорением,
которое в течение t секунд остается неизменным, и проходит за это время путь S = 400
метров. Значение силы (в ньютонах), приложенной в это время к автомобилю, равно \( F=\frac{2mS}{t^2} \)
Определите наибольшее время после начала движения автомобиля, за
которое он пройдет указанный путь, если известно, что сила F, приложенная к
автомобилю, не меньше 10 кН. Ответ выразите в секундах.
Смотреть решение
11. На изготовление 33 деталей первый рабочий тратит на 8 часов меньше, чем
второй рабочий на изготовление 77 таких же деталей. Известно, что первый рабочий
за час делает на 4 детали больше, чем второй. Сколько деталей за час делает второй
рабочий?
Смотреть решение
12. Найдите наименьшее значение функции \( y=x\sqrt{x}-18x+25 \) на отрезке
[25; 625].
Смотреть решение
