1. Света отправила SMS‐сообщения с новогодними поздравлениями своим 19
друзьям. Стоимость одного SMS‐сообщения 1 рубль 90 копеек. Перед отправкой
сообщения на счету у Светы было 37 рублей. Сколько рублей останется у Светы
после отправки всех сообщений?
Смотреть решение
2. На рисунке жирными точками показано суточное количество осадков,
выпадавших в Томске с 8 по 24 января 2005 года. По горизонтали указываются числа
месяца, по вертикали – количество осадков, выпавших в соответствующий день, в
миллиметрах. Для наглядности жирные точки на рисунке соединены линией.
Определите по рисунку, какого числа за данный период впервые выпало ровно 1,5
миллиметра осадков.
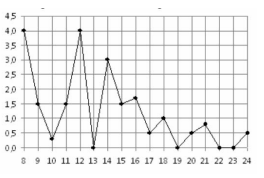
Ответ: 9
3. На клетчатой бумаге изображён круг площадью 60.
Найдите площадь заштрихованного сектора.
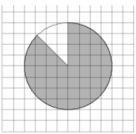
Решение: по рисунку видно, что незаштрихованая часть-это 1/8 всего круга. Значит заштрихованая – 7/8 всего круга. Поэтому \( 60*\frac{7}{8}=52.5 \)
4. Автоматическая линия изготавливает батарейки. Вероятность того, что готовая
батарейка неисправна, равна 0,04. Перед упаковкой каждая батарейка проходит
систему контроля. Вероятность того, что система забракует неисправную батарейку,
равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку,
равна 0,02. Найдите вероятность того, что случайно выбранная изготовленная
батарейка будет забракована системой контроля.
Смотреть решение
5. Найдите корень уравнения \( \frac{x-1}{x+2}=\frac{x-3}{x+4} \)
Смотреть решение
6. В треугольнике ABC угол В равен 68°, угол А равен 59°. AD,
BE и CF – биссектрисы, пересекающиеся в точке O. Найдите
угол ВOF. Ответ дайте в градусах.
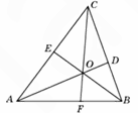
Смотреть решение
8. Площадь боковой поверхности конуса равна 60. Параллельно
основанию конуса проведено сечение, делящее высоту пополам.
Найдите площадь боковой поверхности усеченного конуса.
Смотреть решение
9. Найдите значение выражения \( lg(lg10^\frac{1}{10}) \)
Смотреть решение
10. Скорость автомобиля υ, разгоняющегося с места старта по прямолинейному
отрезку пути длиной l км с постоянным ускорением а км/ч2, вычисляется по формуле
\( V^2=2la \). Определите, с какой наименьшей скоростью будет двигаться автомобиль на
расстоянии 900 метров от старта, если по конструктивным особенностям автомобиля
приобретаемое им ускорение не меньше 2000 км/ч2. Ответ выразите в км/ч.
Смотреть решение
11. Имеется два сплава. Первый содержит 10% никеля, второй – 35% никеля. Из этих
двух сплавов получили третий сплав массой 250 кг, содержащий 25% никеля. На
сколько килограммов масса первого сплава была меньше массы второго?
Смотреть решение
12. Найдите точку максимума функции \( y=(x^2-15x+15)*e^{x+3} \)
Смотреть решение
