13. Дано уравнение \( cosx+\frac{1}{cosx}+cos^2x+tgx^2=0.75 \)
А) Решите уравнение.
Б) Укажите корни этого уравнения, принадлежащие отрезку \( [3pi;4.5pi] \)
Смотреть решение
14. В прямоугольном параллелепипеде ABCDA1B1C1D1 а ребре С1D1 взята
очка К так, что КС1=3КD1
А) Докажите, что плоскость АСК делит диаго и 4:1, считая от точки В.
Б) Найдите расстояние от точки D до пл естно, что АВ=4, ВС=3,
СС1=2.
Смотреть решение
15. Решить неравенство
![]()
Смотреть решение, продолжение 1, * продолжение 2
16. А) Докажите, что сумма углов А, В, С, D, E в вершинах произвольной 5‐конечной
везды равна 180о (рис.1).
Б) Найдите площадь 5‐конечной звезды, вершины которой совпадают с пятью
вершинами правильного шестиугольника, если известно, что сторона последнего
равна 6 (рис. ).
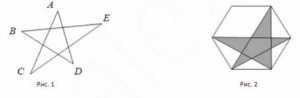
Смотреть решение
18. Найти все а, при каждом из которых уравнение
\( ln(xa^2+xa+2x-x^3)=ln(2x-x^2) \)
имеет ровно один корень.
Смотреть решение
