1. Одна таблетка лекарства весит 20 мг и содержит 5% активного вещества. Ребёнку в
возрасте до 6 месяцев врач прописывает 1,4 мг активного вещества на каждый
килограмм веса в сутки. Сколько таблеток этого лекарства следует дать ребёнку в
возрасте четырёх месяцев и весом 5 кг в течение суток?
Смотреть решение
2. На рисунке жирными точками показана цена тонны никеля на момент закрытия
биржевых торгов во все рабочие дни с 6 по 20 мая 2009 года. По горизонтали
указываются числа месяца, по вертикали — цена тонны никеля в долларах США. Для
наглядности жирные точки на рисунке соединены линией. Определите по рисунку,
какого числа цена тонны никеля на момент закрытия торгов была наименьшей за
указанный период.
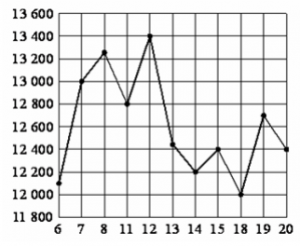
Ответ: 18.
3. Площадь круга, изображённого на клетчатой бумаге,
равна 12. Найдите площадь заштрихованного кругового
сектора.
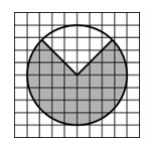
Решение: по рисунку не трудно сказать, что не закрашенная часть круга равна 1/4 от всего круга. Значит закрашенный круг равен 3/4 от всего круга. Три четвертых умножаем на 12=9 Ответ: 9
4. В классе 26 десятиклассников, среди них два близнеца – Фома и Ерёма. Класс
случайным образом делят на две группы по 13 человек в каждой. Найдите
вероятность того, что Фома и Ерёма окажутся в разных группах.
Решение: Вероятность того, что Фома и Ерема окажутся в одной группе равна 12/25=0.48. Соответственно, вероятность того, что они окажутся в разных группах, равна \( 1-0.48=0.52 \)
5. Найдите корень уравнения \( 5^{9+x}=125 \)
Смотреть решение
6. Периметры двух подобных многоугольников
относятся как 3:5. Площадь меньшего многоугольника
равна 18. Найдите площадь большего многоугольника.
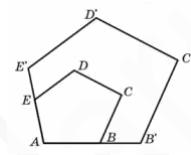
Решение: отношение периметров-это по сути коэффициент подобия этих многоугольников. Мы знаем, что \( k^2=\frac{S1}{S2} \). Где k-коэффициент подобия, то есть отношения периметров (3/5). Составим уравнение. \( (\frac{3}{5})^2=\frac{18}{S2} \) отсюда находим S2 по правилу пропорции. Ответ: 50
8. Во сколько раз увеличится площадь поверхности октаэдра,
если все его ребра увеличить в 3 раза?
Решение: Октаэдр-состоит из 8 граней. Грани-равносторонние треугольники. Площадь равностороннего треугольника \( S=\frac{x^2\sqrt3}{4} \). А всего их 8. Значит площадь поверхности равна S=\( 2x^2\sqrt3 \). x-ребро октаэдра. Если его увеличим в три раза, то получим 3x, да еще в квадрате 9x^2. Делаем вывод, что увеличится в 9 раз.
9. Найдите sin2a, если cosa=0.6 и pi<a<2pi
Смотреть решение
10. По закону Ома для полной цепи сила тока, измеряемая в амперах, равна
\( I=\frac{E}{R+r} \)
где ε — ЭДС источника (в вольтах), r=4 Ом — его внутреннее
сопротивление, R — сопротивление цепи (в омах). При каком наименьшем
сопротивлении цепи сила тока будет составлять не более 5% от силы тока короткого
замыкания \( Ik=\frac{E}{r} \) ? (Ответ выразите в омах.)
Смотреть решение
11. Расстояние между пристанями A и B равно 120 км. Из A в B по течению реки
отправился плот, а через час вслед за ним отправилась яхта, которая, прибыв в пункт
B, тотчас повернула обратно и возвратилась в A. К этому времени плот прошел 24 км.
Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч.
Ответ дайте в км/ч.
Смотреть решение
12. Найдите точку максимума функции \( y=x^3-12x^2+36x-30 \)
Смотреть решение
