13. а) Решите уравнение (1-cos2x)*sin2x=√3sin^2x
б) Укажите корни этого уравнения, принадлежащие отрезку {-П;П/3}
Посмотреть решение
14. В основании треугольной пирамиды ABCD лежит правильный треугольник АВС.
Боковая грань пирамиды BCD перпендикулярна основанию, BD=DC.
а) Постройте сечение пирамиды плоскостью, проходящей через ребро ВС
перпендикулярно ребру AD.
б) Найдите объём пирамиды BCМD, где М – точка пересечения ребра АD и плоскости
сечения, если сторона основания пирамиды ABCD равна 8 √3 а боковое ребро AD
наклонено к плоскости основания под углом 60.
Посмотреть решение
15.
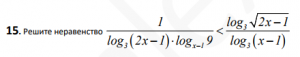
Посмотреть решение
16. В параллелограмме ABCD точка Е – середина стороны АD. Отрезок ВЕ пересекает
диагональ АС в точке Р. АB=PD.
а) Докажите, что отрезок ВЕ перпендикулярен диагонали АС.
б) Найдите площадь параллелограмма, если АВ = 2 см, ВС = 3 см.
Посмотреть решение
17. Джим Хокинс планирует найти сокровища стоимостью 300 тыс. фунтов
стерлингов, которые спрятал капитан Флинт. Перед началом поисков он взял кредит в
размере 10 тыс. фунтов стерлингов у состоятельного сквайера Трелони, чтобы
снарядить шхуну «Испаньола» для поиска сокровищ. Условия кредитования таковы,
что ежемесячно за пользование денежными средствами Джим Хокинс должен
заплатить Трелони 40% от суммы долга, ежемесячные проценты начисляются на тело
долга (каждый месяц Джим платит проценты от 10 тыс. фунтов стерлингов). Через
сколько полных месяцев Джим Хокинс гарантированно планирует найти сокровища,
если после выплаты долга он хочет получить на руки не менее 230 тыс. фунтов
стерлингов? (Джим Хокинс во время поиска сокровищ не может выплачивать долг, а
платит его вместе с процентами после нахождения сокровищ).
Посмотреть решение
