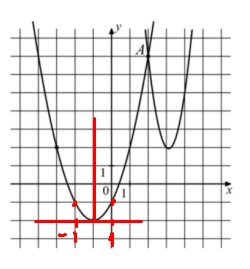
На рисунке изображены графики функций \( f(x)=4x^2-25x+41 \) и \( g(x)=ax^2+bx+c \)которые пересекаются в точках А и В. Найдите ординату точки В.
Решение
Если мысленно переместить систему координат в вершину параболы g(x), то можно легко увидеть, что это обычная \( x^2 \), но здесь система координат расположена по-другому, поэтому осталось понять насколько и куда сместили данную параболу, тогда
\( g(x)=(x+1)^2-2 \) (ее сместили на 1 координату влево и на 2 вниз)
Осталось найти точки пересечения
\( 4x^2-25x+41=(x+1)^2-2 \)
\( x^2-9x+14=0 \)
\( x=2 \) – ее видно на рисунке
\( x=7 \)
\( g(7)=8^2-2=62 \)
Ответ: 62
