Высота правильной четырехугольной пирамиды равна 80 см, сторона основания – 120 см. Найдите площадь сечения, проходящего через центр основания параллельно боковой грани пирамиды.
Решение
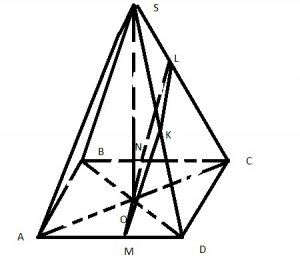
Построим сечение параллельное грани ABS и продящее через центр
Проводим через точку O прямую параллельную AB, далее строим две прямые параллельные боковым ребрам (NL и MK) и соединяем KL как точки лежащие в одной плоскости.
Искомое сечение – р\б трапеция
\( MN=120 \), \( LK=60 \) – как средняя линия
Дальше сторону можно найти из т Пифагора
\( MK=NL=10\sqrt{34} \)
Далее легко ищется плошадь р\б трапеции
Ответ: 45
