Объем треугольной пирамиды равен 135. Точки пересечения медиан всех ее граней являются вершинами второй пирамиды. Найдите ее объем.
Решение
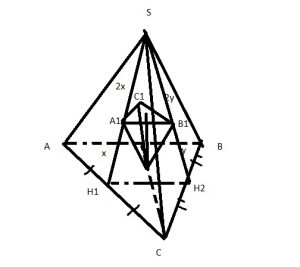
\( H1H2||AB \).
\( H1H2=\frac{AB}{2} \)
медианы в точке пересечения делятся в отношении 2:1, значит из подобия треугольник SH1H2 и SA1B1 можно найти \( A1B1=k*H1H2 \), \( k=\frac{2}{3} \) – коэффициент подобия треугольников
\( A1B1=\frac{2}{3}*\frac{AB}{2}=\frac{AB}{3} \)
Аналогичные рассуждения можно провести с остальными сторонами пирамиды.
Значит все ребра пирамиды будут в 3 раза меньше ребер исходной пирамиды и отсюда следует, что объем искомой пирамиды будет в \( q^3 \) , где \( q=3 \) – (коэф подобия) раза меньше объема исходной пирамиды
\( V_{иск}=\frac{V}{27}=5 \)
Ответ: 5
