Точка, лежащая на окружности верхнего основания цилиндра, соединена с точкой, лежащей на окружности нижнего основания. Угол между проведенной прямой и осью цилиндра составляет 45. Найдите радиус цилиндра, если длина отрезка, соединяющего выбранные точки, равна 7√2, а радиус цилиндра равен его высоте.
Решение
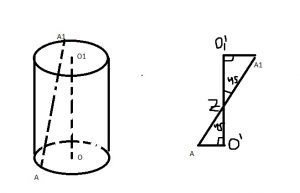
Построим параллельную прямую оси цилиндра O’O1′, получаем, что треугольники AO’Z A1O1’Z равны (они оба прямоугольные, равнобедренные треугольники)
Значит O1’Z=O’Z, значит O1Z=O’Z=r/2, O1A1=r/2 и O’A=r/2 (равнобедренные треугольники)
По т Пифагора \( AZ=\sqrt{2}\frac{r}{2} \)
\( AA1=2AZ=\sqrt{2}r=7\sqrt{2} \)
\( r=7 \)
Ответ: 7
