Найдите объём правильной шестиугольной пирамиды, если её боковое ребро равно 6, а радиус окружности, описанной около основания, равен 3.
Решение
\( V=\frac{1}{3}S_{осн}*h \)
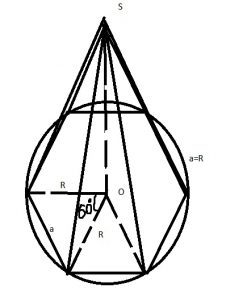
Для простоты можно сделать рисунок, хотя задача почти устная. Помним важное св-во правильный шестиугольной пирамиды – Радиус описанной окружности около основания равен стороне правильной шестиугольной пирамиды (это следует из того что все 6 тругольников, которые образуют шестиугольник – правильные, т.е равносторонние).
\( a=R=3 \)
Осталось только найти высоту пирамиды. Это легко можно сделать по т Пифагора, т.к мы знаем боковую сторону и сторону основания
\( h=\sqrt{36-9}=\sqrt{27}=3\sqrt{3} \)
\( S_{осн}=6S_{правильныхтреуг}=6*\frac{a^2\sqrt{3}}{4} \)
Ответ: 40,5
