В правильной четырехугольной пирамиде боковое ребро равно 12, а тангенс угла между боковой гранью и плоскостью основания равен √7 . Найдите сторону основания пирамиды.
Решение
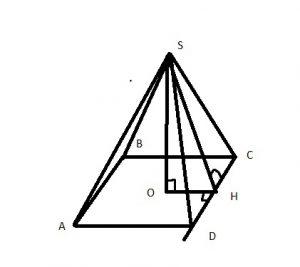
Обозначим сторону основания за \( a \) и Пусть \( \frac{a}{2}=b \)
По условию из прямоугольного треугольника SOH
\( SO=\sqrt{7}b \) (HO=b)
\( SH^2=b^2+7b^2=8b^2 \)
\( 144=b^2+8b^2=9b^2 \) (из SHC)
\( b=4 \)
\( a=8 \)
Ответ: 8
