В треугольную пирамиду вписана сфера радиуса 1. Найдите площадь полной поверхности пирамиды, если ее объем равен 3.
Решение
Знатоки стереометрии сразу вспомнят формулу \( S_{п.п}=\frac{3V}{R} \), где R – радиус вписанной сферы
Но мы ее попробуем вывести
\( V=\frac{1}{3}S_{осн}*h \)
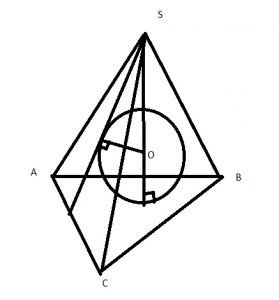
Если обозначить за т. \( O \) – центр вписанной сферы,
\( V=V_{OABC}+V_{OASC}+V_{OBSC}+V_{OASB} \)
\( V_{OABC}=\frac{1}{3}S_{ABC}*R \)
\( V_{OASC}=\frac{1}{3}S_{ASC}*R \)
\( V_{OBSC}=\frac{1}{3}S_{BSC}*R \)
\( V_{OASB}=\frac{1}{3}S_{ASB}*R \)
\( V=\frac{1}{3}R*S_{пол.п} \)
\( S_{полн.п}=\frac{3*3}{1}=9 \)
Ответ: 9
