Дан куб ABCDA1B1C1D1. Через точки B, D и середину ребра D1C1 проведена секущая плоскость. Найдите площадь полной поверхности куба, если площадь сечения равна
2021 ∙ 3.
Решение
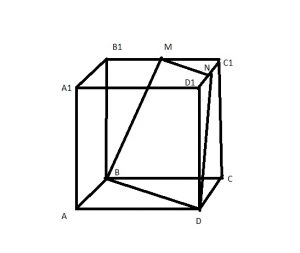
Пусть сторона куба \( a \)
По т Пифагора можно легко найти все стороны нашего сечения (равнобедренной трапеции) BDMN
\( BD=a\sqrt{2} \)
\( MN=\frac{a}{\sqrt{2}} \)
\( BM=\frac{\sqrt{5}}{2}a=BN \)
Проведем высоту трапеции \( MH=\sqrt{\frac{5}{4}a^2-\frac{a^2}{8}}=\frac{3a}{2\sqrt{2}} \)
\( S_{ABCD}=\frac{\frac{a}{\sqrt{2}+a\sqrt{2}}}{2}*\frac{3a}{2\sqrt{2}}=2021*3 \), откуда
\( a^2=\frac{8*2021}{3} \)
\( S_{п.п}=6a^2=2*8*2021=32336 \)
Ответ: 32336
