Основанием пирамиды служит треугольник со сторонами 6, 10 и 14. Каждое из боковых рёбер пирамиды наклонено к основанию под углом 45°. Вычислите объём пирамиды.
Решение
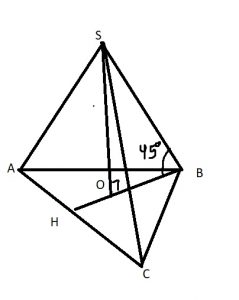
Если все боковые ребра наклонены под одинаковым углом, то высота опускается в центр описанной окружности (это очевидно из треугольников SOB,SOA,SOC, т.к это все прямоугольные равнобедренные треугольники)
\( V=\frac{1}{3}*SO*S_{ABC} \)
\( S_{ABC}=\sqrt{p(p-a)(p-b)(p-c)} \)
\( p=\frac{6+10+14}{2}=15 \)
\( S_{ABC}=15\sqrt{3} \)
Треугольник SOB-р/б, прямоугольный.
\( SO=BO=R \)
Этот радиус можно найти по-разному, самый легкий способ, т.к мы нашли площадь \( R=\frac{abc}{4S}=\frac{14}{\sqrt{3}} \)
\( V=70 \)
Ответ: 70
