Высота правильной треугольной пирамиды в три раза меньше высоты основания пирамиды. Найдите угол между плоскостью боковой грани и плоскостью основания пирамиды. Ответ дайте в градусах.
Решение
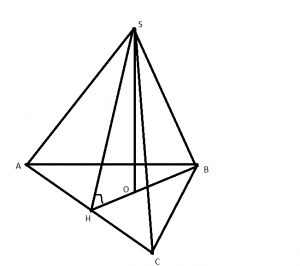
Нам нужно найти двугранный угол \( SACB \), линейный угол этого двугранного угла \( ∠SHB \) – его мы и ищем
Пусть сторона основания равна \( a \)
\( BH=\frac{\sqrt{3}a}{2} \), \( HO=\frac{BH}{3}=\frac{a\sqrt{3}}{6} \) (т O- т пересечения медиан, биссектрис и высот.)
По условию \( SO=\frac{BH}{3}=\frac{a\sqrt{3}}{6} \)
\( tg∠SHO=\frac{SO}{HO}=1 \)
Значит \( ∠SHO=45 \)
Ответ: 45
