Радиус основания цилиндра равен 5, а высота равна 8. Отрезки AB и CDдиаметры одного из оснований цилиндра, а отрезок AA1его образующая. Найдите косинус угла между прямыми A1C и BD, если синус угла CAB равен 0,8.
Решение
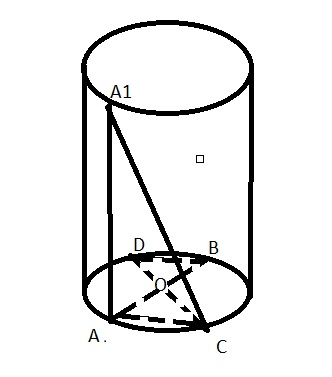
Очевидно, что BD || AC (OD=OB=OA=OC=5) как радиусы окр-ти, получаем два равнобедренных треугольника, два накрест лежащих угла равны, значит прямые параллельны)
А значит мы можем искать угол \( ∠ACA1 \)
Из р/б треугольника AOC, можем легко найти \( AC=6 \) (AO=OC=5 и еще нам дан угол \( cos(∠CAB)=0,8 \)). Попробуй самостоятельно это найти, если не получиться пишите в комменты, вместе разберемся:)
\( A1C=\sqrt{AC^2+AA1^2}=\sqrt{6^2+8^2}=10 \)
А дальше из прямоугольного треугольника A1AC \( cos∠ACA1=\frac{A1C}{AC}=\frac{6}{10}=0,6 \)
Ответ: 0,6
