Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60. Высота пирамиды равна 6. Найдите объем пирамиды.
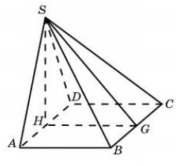
Решение
\( HG=\frac{SH}{tg60}=2\sqrt{3} \)
\( ∠SAD=∠SDA=60 \) (по условию)
значит треугольник SAD -р/б. и \( AB=\frac{2SH}{tg60}=4\sqrt{3} \)
\( V=\frac{1}{3}*4\sqrt{3}*2\sqrt{3}*6=48 \)
Ответ: 48
