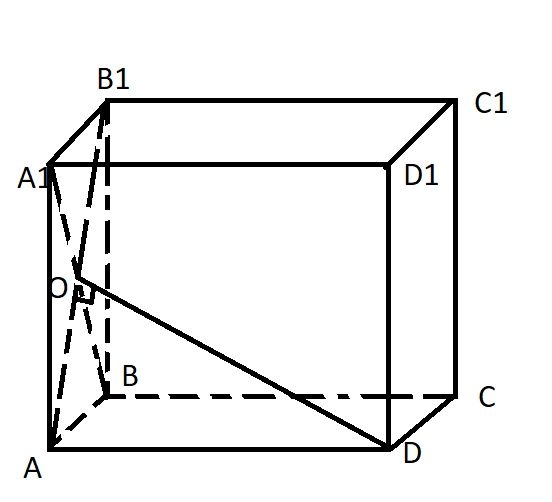
В прямоугольном параллелепипеде АВСDA1В1С1D1 известны отношения длин ребер: АВ : AD : AA1 = 16 : 15 : 34. Расстояние от центра грани АВВ1A1 до вершины D равно 34√2 Найдите сумму длин всех ребер параллелепипеда
Решение
\( AB=16x \), \( AD=15x,AA1=34x \)
Рассмотрим прямоугольный треугольник OAD
\( AO^2+AD^2=OD^2 \)
\( AO=0,5AB1=0,5\sqrt{AB^2+BB1^2} \)
\( AO^2=0,25*1412*x^2=353x^2 \)
\( 353x^2+225x^2=34^2*2 \)
Откуда \( x=2 \)
\( AB+AD+AA1=15*2+16*2+34*2=130 \)
И чтобы найти сумму всех ребер, то умножаем это число на 4
Ответ: 520
