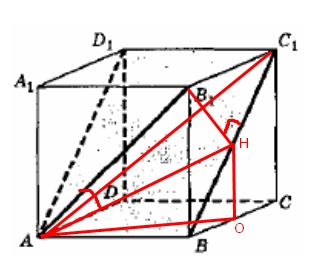
В кубе ABCDA1B1C1D1 найдите угол между прямой АВ1и плоскостью АВС1. Ответ дайте в градусах.
Решение
Проведем перпендикуляр BH на BC1, BH-перпендикулярна всей плоскости (AD1C1B), т.к плоскость ABC1 содержится в ней, то и BH перпендикулярна ABC1
Угол между прямой и плоскостью – это угол между проекцией прямой на эту плоскость и самой прямой
Искомый угол \( ∡B1AH \) (AH-проекция)
Пусть сторона куба \( a \)
найдем все стороны этого треугольника
\( B1H \) – это 1/2 диагонали квадрата \( B1H=\frac{a\sqrt{2}}{2} \)
\( AB1=\sqrt{2}a \) – диагональ квадрата
\( AH=\sqrt{AO^2+HO^2} \)
\( HO=\frac{a}{2} \)
\( AO=\sqrt{a^2+\frac{a^2}{4}}=\frac{\sqrt{5}a}{2} \)
Значит \( AH=\frac{\sqrt{6}a}{2} \)
По т косинусов
\( cos∡B1AH=\frac{AH^2+AB1^2-B1H^2}{2*AH*AB1} \)
Подставляем все в формулу \( cos∡B1AH=\frac{\sqrt{3}}{2} \) значит \( ∡B1AH=30 \)
Ответ: 30
