В правильной треугольной пирамиде SABC сторона основания \( AB=8\sqrt{3} \), а боковое ребро \( SA=\sqrt{73} \) Найдите расстояние от точки В до плоскости SAC.
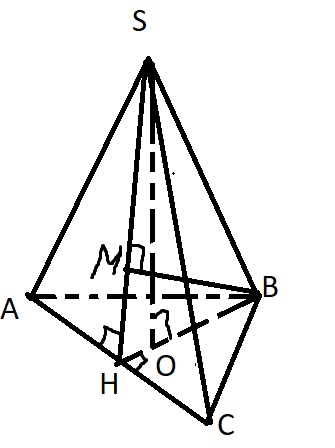
Решение
Нам нужно провести перпендикуляр из точки B на плоскость SAC
Для этого проведем BH-высота правильного треугольника и проведем апофему SH на AC. Так же проведем перпендикуляр BM на SH
Если прямая перпендикулярна двум пересекающимся прямым лежащих в плоскости, то эта прямая перпендикулярна данной плоскости
\( BM⊥SH \) – мы так провели данную прямую:)
\( BM⊥AC \) – по т о 3-х перпендикулярах
Значит BM – есть искомое расстояние
Начинаем с конца
\( BM=sin(∡SHB)*BH \)
\( BH=\sqrt{64*3-16*3}=12 \)
Осталось найти синус:)
точка O – точка пересечения медиан, биссектрис и высот, т.к треугольник правильный!
\( OH=\frac{1}{3}BH=4 \) и \( BO=\frac{2}{3}BH=8 \)
\( sin(∡SHB)=\frac{SO}{SH} \) (из прямоугольного треугольника SOH)
\( SH=\sqrt{73-16*3}=5 \)
\( SO=\sqrt{SH^2-OH^2}=3 \)
Значит
\( sin(∡SHB)=\frac{3}{5} \)
\( BM=sin(∡SHB)*BH=\frac{3}{5}*12=7,2 \)
Ответ: 7,2
