Высота основания правильной треугольной пирамиды равна 9, а высота боковой грани пирамиды, проведенная к ребру основания, равна √73. Найдите боковое
ребро пирамиды.
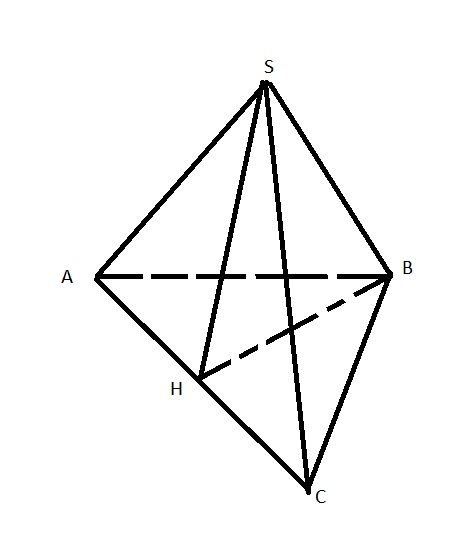
Решение
\( BH=9 \) – по условию. Пусть \( a \) – сторона основания. \( BH^2=-\frac{a^2}{4}+a^2 \), откуда \( a^2=108 \)
\( AS^2=AH^2+SH^2=\frac{a^2}{2}+73=100 \)
\( AS=10 \)
Ответ: 10
