Площадь сечения правильной треугольной пирамиды плоскостью, проходящей через боковое ребро и середину противолежащей стороны основания, равна 15. Найдите объем пирамиды, если сторона ее основания равна 4.
Решение
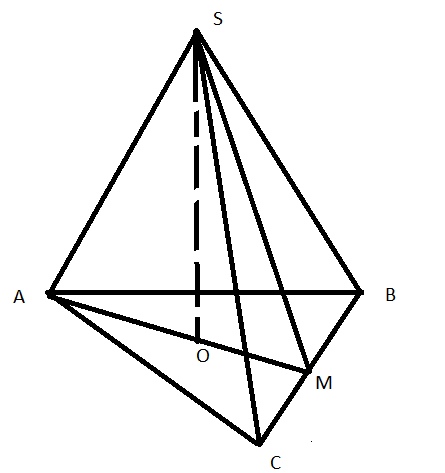
Сечение, проходящей через боковое ребро и середину противолежащей стороны основания – это треугольник \( AMS \)
\( S_{AMS}=15=0,5*SO*AM \)
\( AM=\sqrt{4^2-2^2}=2\sqrt{3} \)
\( SO=\frac{15}{\sqrt{3}} \)
\( V=\frac{1}{3}*SO*S_{осн} \)
\( S_{осн}=\frac{4^2\sqrt{3}}{4} \)
\( V=20 \)
Ответ: 20
