Через точку окружности основания цилиндра проведены два сечения: одно через ось цилиндра, а второе параллельно ей. Угол между плоскостями сечений равен 45°. Площадь боковой поверхности цилиндра равна 18pi√2. Найдите меньшую из площадей данных сечений.
Решение
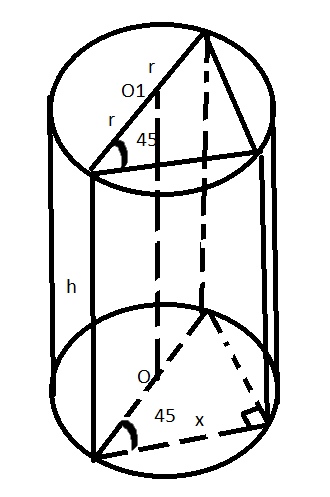
\( S_{б}=2\pi rh=18\pi \sqrt{2} \)
\( 2rh=18\sqrt{2} \)
\( S_{1}=2rh=18\sqrt{2} \) – площадь осевого сечения
Из прямоугольного треугольника в основании (т.к вписанный угол опирается на диаметр). находим \( cos45=\frac{x}{2r} \)
\( \frac{xh}{18\sqrt{2}}=\frac{1}{\sqrt{2}} \)
\( hx=18 \) – это и есть площадь второго сечения
Ответ: 18
