Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен √3, если известно, что высота призмы равна 6.
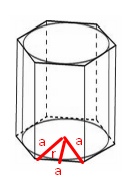
Решение
по т Пифагора \( a=\sqrt{r^2+\frac{a^2}{4}} \)
\( \frac{3}{4}a^2=r^2 \)
\( a=\frac{2r}{\sqrt{3}} \)
\( a=2 \)
\( S_{бок}=6*a*h=6*2*6=72 \)
Ответ: 72
