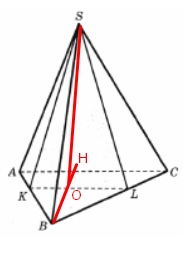
В правильной треугольной пирамиде SABC ребра ВА и ВС разделены точками K и L так, что ВК=BL=4 и KA=LC=2. Найдите угол между плоскостью основания АВС и плоскостью сечения SKL. Ответ выразите в градусах.
Решение
Пусть \( SO \) – высота пирамиды, опускается в центр основания
Если мы докажем, что точка O содержится в плоскости SKL, то плости SKL и ABC будут перпендикулярны, т.к SO перпендикулярна основанию по условию
\( BH \) – высота, биссектриса, медиана
Треугольники \( BKL \) и \( BAC \) подобны по 2 признаку подобия
\( \frac{BO}{BH}=\frac{BL}{BC}=\frac{2}{3} \)
и значит точка O делит нашу медиану в отношении 2:1 и следовательно мы выбрали положение точки O (на прямой KL) правильно, следовательно SO принадлежит плоскости SKL и следовательно плоскости ABC и SKL перпендикулярны.
Ответ: 90
