Найдите объём треугольной пирамиды DABC, если AB=30, BC =CA=17 и двугранные углы при основании равны 45.
Решение
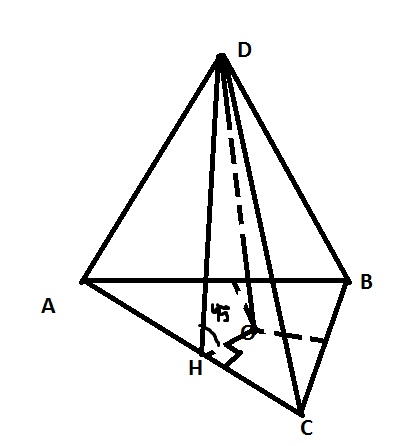
Если двугранные углы равны между собой (а это углы между высотами боковых граней и плоскостью основания), значит проекции этих высот на основание также равны и, следовательно, высота пирамиды D проецируется в точку О – центр вписанной в основание окружности.
\( V=\frac{1}{3}*S_{осн}*h \)
\( S_{осн}=0.5*AB*h1 \) , \( h1=\sqrt{17^2-15^2}=8 \) (т.к треугольник равнобедренный и значит высота опускается в середину AB)
\( S_{осн}=120 \)
\( S_{осн}=p*r=\frac{30+17+17}{2}*r=120 \)
\( r=\frac{15}{4} \)
Треугольник DOH -р/б, значит \( HO=OD=r=h=3,75 \)
\( V=\frac{1}{3}*120*\frac{15}{4}=150 \)
Ответ: 150
