Все плоские углы при вершине правильной треугольной пирамиды прямые. Найдите площадь боковой поверхности пирамиды, если площадь её основания равна 18√3.
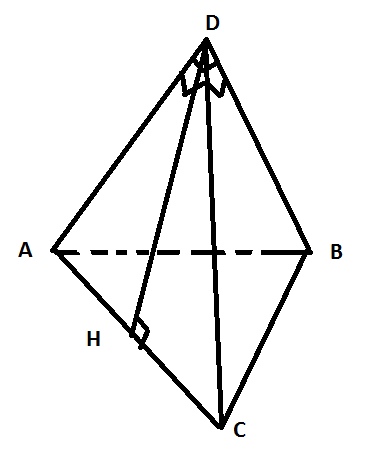
Решение
\( S_{бок}=3S_{ADC} \)
\( a \)-сторона правильного треугольника (основания)
\( S_{ABC}=\frac{a^2\sqrt{3}}{4}=18\sqrt{3} \)
\( a=6\sqrt{2} \)
треугольник ADC-равнобедренный и прямоугольный по условию
\( DH=tg45*AH=1*3\sqrt{2} \)
\( S_{ADC}=0,5*6\sqrt{2}*3\sqrt{2}=18 \)
\( S_{бок}=3*18=54 \)
2 способ:
Если все плоские углы при одной из вершин тетраэдра —прямые, то квадрат площади грани, противолежащей этой вершине, равен сумме квадратов площадей остальных граней.
Тогда решение куда легче:)
Ответ: 54
