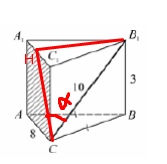
В прямой призме АВСА1В1С1 АВ=ВС, СВ1=10, ВВ1=3, АС=8. Найдите угол в градусах между прямой СВ1 и плоскостью АА1С.
Решение
Проведем из точки B1 высоту B1H – она перпендикулярна плоскости AA1C. (т.к B1H⊥A1C1 и C1C⊥BB1 (т.к прямая призма и высота перпендикулярна основаниям)).
Получаем, что угол \( ∡B1CA \) – искомый угол, между прямой и ее проекцией на плоскость (т о 3-х перпендикулярах)
\( CB=AB=\sqrt{91} \)-по т Пифагора
\( B1H=\sqrt{91-16}=\sqrt{75} \) (из равнобедренного треугольника по т Пифагора)
\( sina=\frac{\sqrt{75}}{10}=\frac{\sqrt{3}}{2} \)
\( a=60 \)
Ответ: 60
