В правильной четырехугольной призме ABCDA1B1C1D1 ребро АА1 равно 10 , а стороны основания равны 8. Найдите площадь сечения призмы плоскостью, проходящей через точки А1 , С1 и середину ребра АВ.
Решение
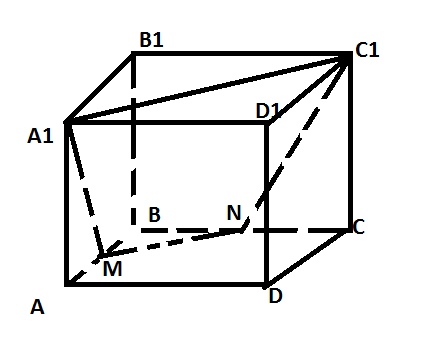
Строим сечение, соед т A1 и M, т.к лежат в одной плоскости, проводим прямую параллельную A1C1, если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны, и соединяем NC1. И получаем трапецию.
Все стороны находится по т Пифагора
\( A1M=\sqrt{26}=C1N \)
\( A1C1=8\sqrt{2} \)
\( MN=4\sqrt{2} \)
Дальше легко найти высоту, т.к трапеция равнобедренная \( h=3\sqrt{2} \)
\( S=\frac{4\sqrt{2}+8\sqrt{2}}{2}*3\sqrt{2}=36 \)
Ответ: 36
