Дан параллелепипед ABCDA1B1C1D1, в основании которого лежит прямоугольник
ABCD, AB=45, BC =24. Найдите расстояние от точки A1 до прямой CC1, если высота
параллелепипеда равна 20, а боковое ребро равно 34
Решение
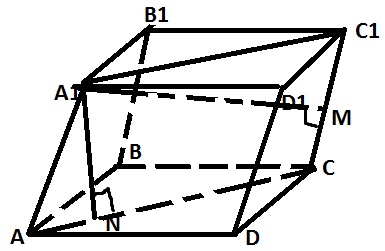
Искомое расстояние – это высота \( A_{1}M \)
Рассмотрим параллелограмм \( AA1CC1 \)
\( A_{1}M \) – это высота в нем
\( A_{1}N \) – высота параллелограмма, \( A_{1}N=20 \)
\( S_{AA1CC1}=A_{1}N*AC \)
и с другой стороны
\( S_{AA1CC1}=A_{1}M*CC1 \)
\( AC=\sqrt{45^2+24^2}=51 \) – по т Пифагора
\( 20*51=34*A_{1}M \)
\( A_{1}M=30 \)
Ответ: 30
